题目

（本小题满分12分）
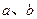
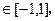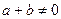设f(x)是定义在[-1,1]上的奇函数，对于任意的 当时，都
有
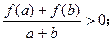
（1）若函数g(x)=f(x-c)和h(x)=f(x-c²)的定义域的交集是空集，求c的取值范围；
（2）判断函数f(x)在[-1,1]上的单调性，并用定义证明。

答案

（1）{x|c＜-1或c＞2}
（2）增函数

解析

（1）由-1≤x-c≤1得g(x)定义域：c-1≤x≤1+c
由-1≤x-c²≤1得f(x)定义域：c²-1≤x≤1+c² -------------------------4分
由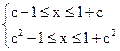得：c+1＜c²-1 或c²+1＜c-1解得：C＜-1或C＞2---5分
综上：C的取值范围为{x|c＜-1或c＞2}------------------------------------6分
（2）任取x₁、x₂Î[-1，1],且 x₁＜x₂，
则f(x₁)-f(x₂)=f(x₁)+f(-x₂)=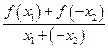·(x₁-x₂) --------------------------8分
由已知有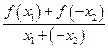：＞0，而x₁-x₂＜0 ∴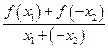·(x₁-x₂) ＜0
∴f(x₁) ＜f(x₂) ----------------------------------------------------10分
∴f(x)在[-1，1]上为增函数，  ------------------------------------12分