题目

已知函数，且f（4）=3．
（1）判断f（x）的奇偶性并说明理由；
（2）判断f（x）在区间（0，+∞）上的单调性，并证明你的结论；
（3）若在区间[1，3]上，不等式f（x）＞2x+2m+1恒成立，试确定实数m的取值范围．

答案

解：（1）由f（4）=3得：n=1
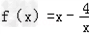∴，其定义域为（﹣∞，0）∪（0，+?）
又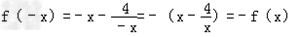
∴函数f（x）在（﹣∞，0）∪（0，+∞）上为奇函数．
（2）函数f（x）在（0，+∞）上是增函数，
证明如下：任取x₁，x₂，且0＜x₁＜x₂，
则x₁﹣x₂＜0，x₁x₂＞0
那么=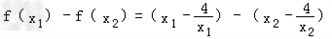
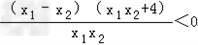
即f（x₁）＜f（x₂）
∴函数f（x）在（0，+∞）上是增函数．
（3）由f（x）＞2x+2m+1，
得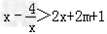
∴2m+1
∴当x∈[1，3]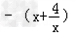，的最小值是﹣5，
∴2m+1＜﹣5，得m＜﹣3，
所以实数m的取值范围是（﹣∞，﹣3）．

解析