题目
(Ⅰ)讨论函数f(x)的奇偶性;
(Ⅱ)若a<0,c=-2,方程f(x)=x的两实根x1,x2满足:x1∈(0,1),x2∈(1,2),求证:-4<
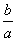 <-1。
<-1。 答案
当b=0时,f(x)=ax2+c(x∈R,a≠0),满足f(-x)=f(x),所以f(x)是偶函数;
当b≠0时,f(x)=ax2+bx+c(x∈R,a≠0),不满足f(-x)=f(x),也不满足f(-x)=-f(x),
所以f(x)是非奇非偶函数.
(Ⅱ)证明:由方程f(x)=x,得ax2+(b-1)x-2=0,
又两实根x1,x2满足x1<1<x2<2,
则a+b-1-2>0,即:a+b-3>0, ①
4a+2(b-1)-2<0,即:2a+b-2<0,②
由①×2+②×(-3)可得出-4a-b>0,
∵a<0,
∴
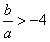 ,
,又由①可得出
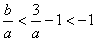 ,故
,故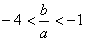 。
。