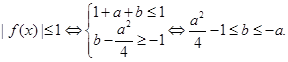题目
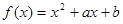 .
.(1)若对任意的实数
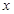 ,都有
,都有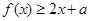 ,求
,求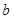 的取值范围;
的取值范围;(2)当
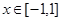 时,
时,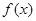 的最大值为M,求证:
的最大值为M,求证: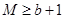 ;
;(3)若
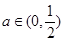 ,求证:对于任意的
,求证:对于任意的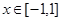 ,
,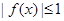 的充要条件是
的充要条件是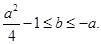
答案
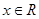 ,都有
,都有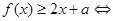
对任意的
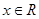 ,
,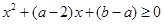
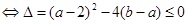
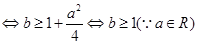 ∴
∴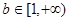 .
.(2)证明:∵
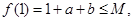
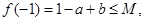 ∴
∴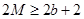 ,即
,即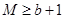 。
。(3)证明:由
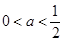 得,
得,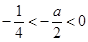 ∴
∴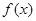 在
在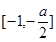 上是减函数,在
上是减函数,在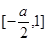 上是增函数。∴当
上是增函数。∴当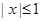 时,
时,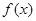 在
在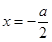 时取得最小值
时取得最小值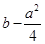 ,在
,在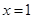 时取得最大值
时取得最大值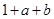 .
.故对任意的
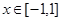 ,
,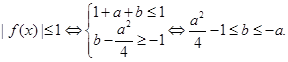
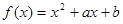 .
.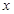 ,都有
,都有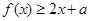 ,求
,求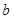 的取值范围;
的取值范围;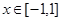 时,
时,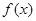 的最大值为M,求证:
的最大值为M,求证: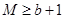 ;
;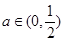 ,求证:对于任意的
,求证:对于任意的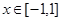 ,
,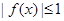 的充要条件是
的充要条件是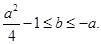
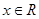 ,都有
,都有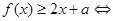
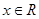 ,
,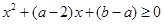
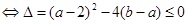
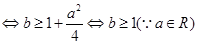 ∴
∴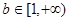 .
.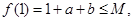
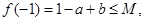 ∴
∴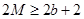 ,即
,即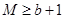 。
。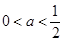 得,
得,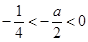 ∴
∴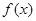 在
在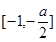 上是减函数,在
上是减函数,在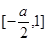 上是增函数。∴当
上是增函数。∴当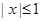 时,
时,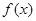 在
在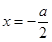 时取得最小值
时取得最小值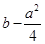 ,在
,在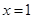 时取得最大值
时取得最大值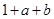 .
.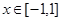 ,
,