题目

判断下列函数的奇偶性：
（1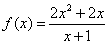）；（2）f(x)=a(x∈R)；（3）。

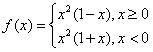答案

解：（1）函数的定义域为{x|x≠-1}，不关于原点对称，所以f(x)既不是奇函数也不是偶函数；
（2）函数的定义域为R，当a=0时，f(x)既是奇函数又是偶函数；
当a≠0时，f(-x)=a=f(x)，即f(x)是偶函数；
（3）函数的定义域为R，当x＞0时，-x＜0，
此时f(-x)=(-x)²[1+(-x)]=x²(1-x)=f(x)；
当x＜0时，-x＞0，此时f(-x)=(-x)²[1-(-x)]=x²(1+x)=f(x)；
当x=0时，-x=0，此时f(-x)=0，f(x)=0，即f(-x)=f(x)；
综上，f(-x)=f(x)，所以f(x)为偶函数。

解析