题目
已知函数f ( x )=x 2+ax+b
(1)若f (x)在[ 1,+∞)内递增,求实数a的范围。
(2)若对任意的实数x都有f (1+x)="f" (1-x) 成立,
①求实数 a的值;
②证明函数f(x)在区间[1,+∞
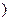 上是增函数.
上是增函数.
答案
解析
(2)由f(1+x)=f(1
 -x)得,
-x)得,(1+x)2+a(1+x)+b=(1-x)2+a(1-x)+b,即:(a+2)x=0,
由于对任意的x都成立,∴
 a=-2.
a=-2.可知 f (x)=x 2-2x+b,下面证明函数f(x)在区间[1,+∞
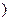 上是增函数.设
上是增函数.设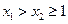 ,
,则
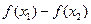 =(
=(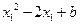 )-(
)-(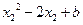 )
)=(
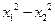 )-2(
)-2(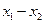 )=(
)=(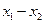 )(
)(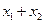 -2)
-2)∵
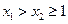 ,则
,则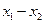 >0,且
>0,且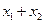 -2>2-2=0,
-2>2-2=0,∴
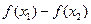 >0,即
>0,即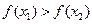 ,故函数f(x)在区间[1,+∞
,故函数f(x)在区间[1,+∞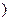 上是增函数.
上是增函数. 法2
 :可用导数证明
:可用导数证明
