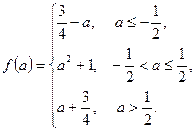题目
 为实数,函数
为实数,函数 ,
, .
. (1)讨论
 的奇偶性; (2)求
的奇偶性; (2)求  的最小值.
的最小值.
答案
 既不是奇函数,也不是偶函数。
既不是奇函数,也不是偶函数。(2)
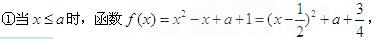
若
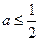 ,则函数
,则函数 在
在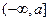 上单调递减,∴函数
上单调递减,∴函数 在
在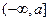 上的最小值为
上的最小值为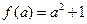 ;
;若
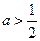 ,函数
,函数 在
在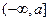 上的最小值为
上的最小值为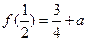 ,且
,且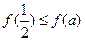 .
.②当
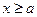 时,函数
时,函数
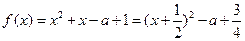 ,
,若
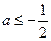 ,则函
,则函 数
数 在
在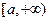 上的最小值为
上的最小值为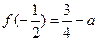 ,且
,且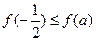 ;
;若
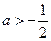 ,则函数
,则函数 在
在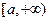 上单调递增,∴函数
上单调递增,∴函数 在
在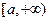 上的最小值
上的最小值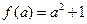 .
.综上,
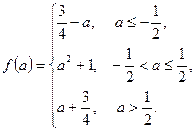
 为实数,函数
为实数,函数 ,
, .
.  的奇偶性; (2)求
的奇偶性; (2)求  的最小值.
的最小值.
 既不是奇函数,也不是偶函数。
既不是奇函数,也不是偶函数。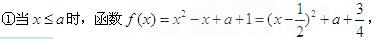
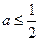 ,则函数
,则函数 在
在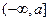 上单调递减,∴函数
上单调递减,∴函数 在
在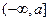 上的最小值为
上的最小值为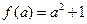 ;
;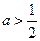 ,函数
,函数 在
在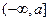 上的最小值为
上的最小值为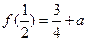 ,且
,且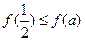 .
.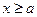 时,函数
时,函数
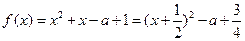 ,
,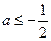 ,则函
,则函 数
数 在
在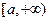 上的最小值为
上的最小值为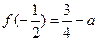 ,且
,且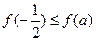 ;
;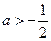 ,则函数
,则函数 在
在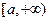 上单调递增,∴函数
上单调递增,∴函数 在
在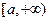 上的最小值
上的最小值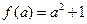 .
.