题目
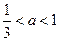 ,若
,若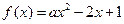 在区间
在区间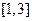 上的最大值为
上的最大值为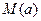 ,最小值为
,最小值为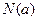 ,记
,记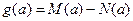 .
.(1)求
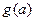 的解析表达式; (2)若对一切
的解析表达式; (2)若对一切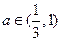 都有
都有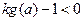 成立,求实数
成立,求实数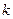 的取值范围.
的取值范围.
答案
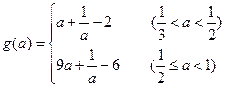 (Ⅱ)
(Ⅱ) 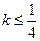
解析
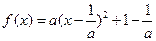
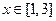
由
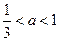 知,
知,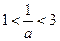 .从而
.从而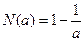
∴当
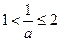 即
即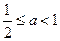 时,
时, 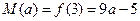
当
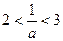 即
即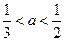 时,
时,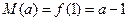
∴
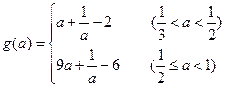
(2)当
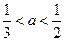 时,
时,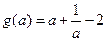 为减函数.∴
为减函数.∴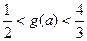 .
.要使
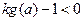 恒成立,则
恒成立,则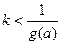 恒成立.而
恒成立.而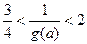 ∴
∴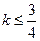 .
.又当
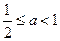 时,
时,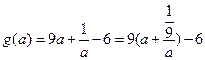 为增函数∴
为增函数∴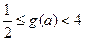
要使
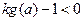 恒成立.则
恒成立.则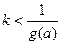 恒成立.而
恒成立.而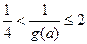 ∴
∴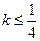
综上得,
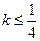 .
.
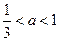 ,若
,若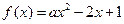 在区间
在区间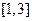 上的最大值为
上的最大值为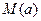 ,最小值为
,最小值为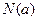 ,记
,记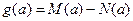 .
.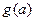 的解析表达式; (2)若对一切
的解析表达式; (2)若对一切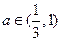 都有
都有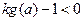 成立,求实数
成立,求实数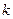 的取值范围.
的取值范围.
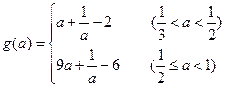 (Ⅱ)
(Ⅱ) 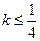
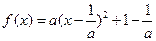
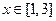
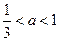 知,
知,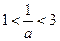 .从而
.从而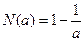
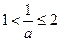 即
即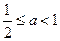 时,
时, 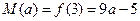
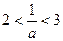 即
即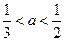 时,
时,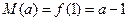
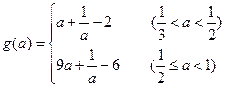
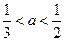 时,
时,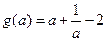 为减函数.∴
为减函数.∴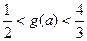 .
.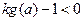 恒成立,则
恒成立,则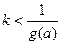 恒成立.而
恒成立.而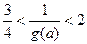 ∴
∴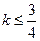 .
.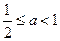 时,
时,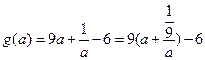 为增函数∴
为增函数∴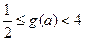
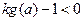 恒成立.则
恒成立.则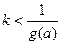 恒成立.而
恒成立.而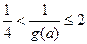 ∴
∴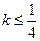
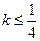 .
.