题目
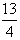 的图象上的一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,这一系列点的横坐标构成以-
的图象上的一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,这一系列点的横坐标构成以-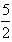 为首项,-1为公差的等差数列{xn}。
为首项,-1为公差的等差数列{xn}。(1)求点Pn的坐标;
(2)设抛物线C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,对于n∈N*,第n条抛物线Cn的顶点为Pn,抛物线Cn过点Dn(0,n2+1),且在该点处的切线的斜率为kn,求证:
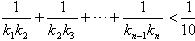 。
。答案
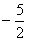 为首项,-1为公差的等差数列{xn},故
为首项,-1为公差的等差数列{xn},故 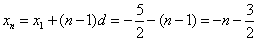
又
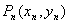 位于函数
位于函数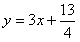 的图象上
的图象上所以
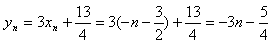
所以点
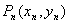 的坐标为
的坐标为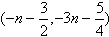 。
。(2)由题意可设抛物线Cn的方程为
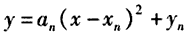
即
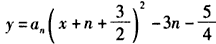
由抛物线Cn过点
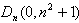
于是有n2+1=
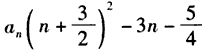
由此可得
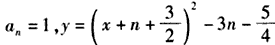
故
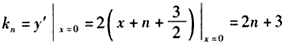
所以
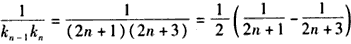 (n≥2)
(n≥2)于是
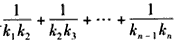
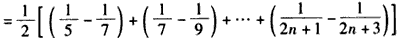
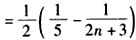
故
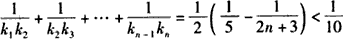 。
。